A beszéden kívül léteznek más univerzális nyelvek, amiket itt szeretnék röviden bemutatni.

A matematika az emberiség legrégebben használt közös nyelve. Bár az elején még bizonyos kultúrák másképp jelölték a számokat, manapság már elfogadottá vállt egy standard.

A mostani számokat az arab világból vettük át, akik az indiaiaktól kölcsönözték őket. Az ókorban az arab világ számított a természettudományok birodalmának.

A római számokat ugyebár mindenki ismeri és manapság is széles körben használják, bár nem számolásra, hanem jelölésre. Érdekességük, hogy a nullának nincs szimbóluma.

Nem csoda, hiszen a nulla fogalma későbbről származik. A nulla számjegy első bizonyított használata a 9. századból származik, bár akkoriban a jele még egy pont volt.

A tizes számrendszer sem volt mindenhol elterjedt az ókorban. A sumérok például hatvanas rendszerben számoltak.

Tőlük örököltük a 24 órás napot, a hatvan perces órákat, valamint a 360 fokos kör fogalmát is.

Ezzel ellentétben a mayák huszas rendszerben számoltak. Náluk az egyest egy ponttal jelőlték, míg a négyest négy ponttal.

Az ötös viszont egy vízszintes vonal volt, majd a hatos egy vonal és egy pont felette. Ez így ment egészen a kilencesig, ami egy vonal felett négy pont volt, viszont a tízet már két vonallal írták.

Az így leírható maximum a 19-es volt, vagyis három vonal felett négy pont. A nehezebb dolog most kezdődik. Ezt egy Wikipédiáról lopott ábrával próbálom vizualizálni.

 

 

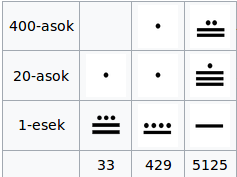
Az ábrán a 33-as, 429-es és az 5.125-ös szám van leírva. A húsz feletti számokat egymás alá írt számjegyekkel reprezentálták.

Számukra a 20-as és a 400-as számok olyanok voltak, mint nekünk a 10-es és a 100-as. Ezt a komplikált számrendszert elnézve, valószínűnek tartom, hogy a társadalom főleg húsz alatti számokkal dolgozott.

Megosztás a facebookon